地学统计

地学统计可通过检查不同的采样位置对来探索数据的空间自相关性。如果存在空间相关性，则距离较近的点对应具有较小的差值。随着各个点之间的距离越来越大，差值的平方也应随之增大。平方差超过某个距离后就会保持不变，超过这个距离的位置对被视为不相关。

地统计方法的基本假设是，对于任意两个彼此间的距离和方向都相近的位置，其差值的平方也应相近。这种关系称为平稳性。

地统计方法不仅具有产生预测表面的功能，而且能够对预测的确定性或准确性提供某种度量。

空间权重矩阵

功能说明

用于构建空间权重矩阵文件，用表示数据集中各要素之间的空间关系。通过已知有限的采样点数据，推求任意点数据，常用于根据离散采样点获取连续预测表面；栅格像元值表示数据集中各要素之间的空间关系。

操作说明

1. 点击【地学统计】-【空间权重矩阵】，弹出空间权重矩阵对话框；

2. 在弹出的对话框中选择点简单要素类，设置相关参数，设置目标路径；

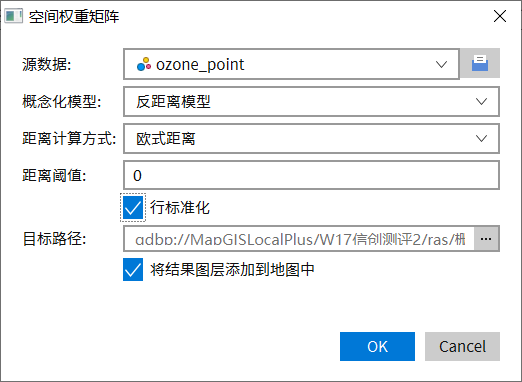
• 【数据源】：当数据源类型不同时，概念化模型也不同。
• 【概念化模型】：
  • 反距离模型：所有要素均被视为所有其他要素的相邻要素，所有要素都会影响目标要素，但是随着距离的增加，影响会越小，要素之间的权重为距离分之一，适用于连续数据。
  • 反平方距离模型：与“反距离模型”相似,随着距离的增加，影响下降的更快，要素之间的权重为距离的平方分之一。
  • 固定距离阈值模型：适用于点数据、及面大小变化较大的面数据。
  • 区域距离反比模型：适用于存在相邻边、相交的面数据。
  • 面邻接模型：适用于有邻接点、相邻边、相交的面数据。
• 【距离计算方式】：
  • 欧氏距离：一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。
  • 曼哈顿距离：是种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。
• 【距离阈值】：自定义输入距离阈值。0表示为未应用任何距离，则每个要素都是相邻要素。非零正值表示当要素间的距离小于此值时为相邻要素。

3. 点击"确定"，执行分析，结果会生成一个空间权重栅格文件。

空间相关性

功能说明

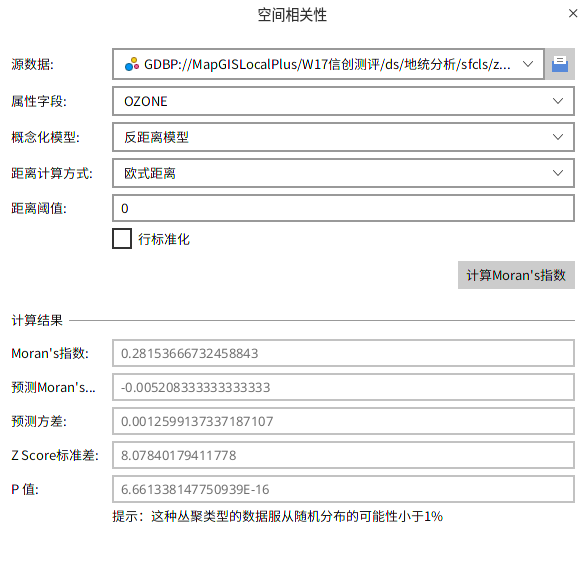
根据指定的要素及相关属性，使用全局莫兰指数统计量评估要素所表达的模式是聚类模式、离散模式还是随机模式。

空间自相关 (Global Moran's I) 工具计算了指数值后，将计算期望指数值。然后，将期望指数值与观察指数值进行比较。在给定数据集中的要素个数和全部数据值的方差的情况下，该工具将计算z得分和p值，用来指示此差异是否具有统计学上的显著性。

操作说明

1. 点击【地学统计】-【空间相关性】，弹出空间自相关对话框；

2. 在弹出的对话框中选择点简单要素类，设置相关参数，设置目标路径：

• 【数据源】：设置待分析的矢量数据集，支持点、线、面三种类型的数据集。建议源数据中的对象个数大于或等于30，以保证结果的可靠性。
• 【概念化模型】：
  • 反距离模型：所有要素均被视为所有其他要素的相邻要素，所有要素都会影响目标要素，但是随着距离的增加，影响会越小，要素之间的权重为距离分之一，适用于连续数据。
  • 反平方距离模型：与“反距离模型”相似,随着距离的增加，影响下降的更快，要素之间的权重为距离的平方分之一。
  • 固定距离阈值模型：适用于点数据、及面大小变化较大的面数据。
  • 区域距离反比模型：适用于存在相邻边、相交的面数据。
  • 面邻接模型：适用于有邻接点、相邻边、相交的面数据。
• 【距离计算方式】：空间统计分析中有两种距离，分别是欧式距离和曼哈顿距离。
• 【距离阈值】：用户自定义距离阈值。

3. 点击【计算Moran's指数】，执行分析，显示计算结果。

空间自相关分析结果会返回：Moran's I 指数、期望值、方差、Z得分、 P值五个参数，使用 z 得分或 p 值指示统计显著性时，则可以拒绝零假设，如果 Moran's I 指数值为正值，就表示这份数据具有空间正相关性，数据集用于分析的值与空间聚集度成正比；如果 Moran's I 指数值为负则指示离散趋势。

克里格插值

功能说明

克里金法假设至少在自然现象中观察到的某些空间变化可借助带有空间自相关的随机过程进行建模，并要求对空间自相关进行显式建模。克里金插值是以数据的空间自相关性为基础，使用变异函数模型，对有限区域内的未知样本点进行无偏估计的插值方法。在样本点存在空间自相关性或者方向性趋势时，克里金是最合适的插值方法。同一个分布区内的样点数据之间存在的空间自相关性，距离越近的两个样点之间，相关性越强。目前克吕金插值方法，在地理信息和气象学、地矿学、铜产储量分析方面有着广泛的应用。

操作说明

1. 点击【地学统计】-【克里格插值】，弹出克里格插值对话框，分别有【变异函数】模块和【搜索椭球】模块；

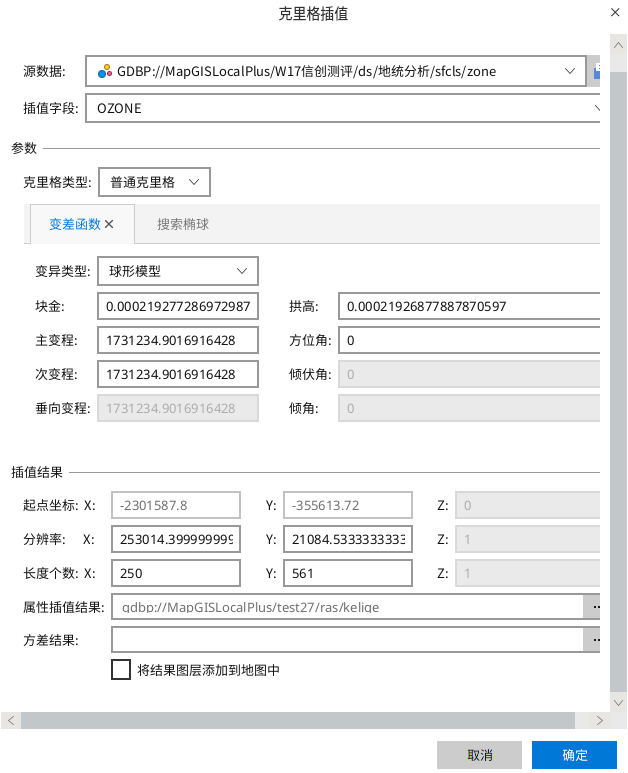
2. 设置弹出的对话框中属性，部分属性展开类型有：

• 【克里格类型】：
  • 【普通克里格】：满足二阶平稳（或本征）假设的区域化变量，普通克里金法是使用最普通和广泛的克里金方法。该方法假定用于插值的字段值的期望（平均值）未知且恒定。
  • 【简单克里格】：简单克里金法使用的数据应符合数据变化成正态分布的前提假设。该方法假定用于插值的字段值的期望（平均值）已知的某一常数。简单克吕金插值方法不适用于对具有局部趋势情况的样点数据进行插值。
  • 【泛克里格】：泛克里金法使用的数据应符合数据变化成正态分布的前提假设。非平稳或具有飘逸存在的区域化变量。该方法假定用于插值的字段值的期望（平均值）未知的变量。
• 【变异类型】：总共有球型模型、指数模型、高斯模型、线性模型、空穴模型五种变异类型。
• 【插值结果】：输出结果为栅格数据集，设置栅格分辨率和结果存储路径。

3. 点击【ok】，执行分析，显示插值结果。颜色越深表示预测值比较大，比如预测该区域内臭氧浓度高，颜色浅或像元值小的表示臭氧浓度低。

协方差函数

功能说明

协方差函数将邻近事物比远处事物更相似这一假设加以量化。协方差将统计相关性的强度作为距离函数来测量。对协方差函数建模的过程将协方差曲线与经验数据拟合，目标是达到最佳拟合，并将对现象的认知纳入模型，之后模型便可用于预测。

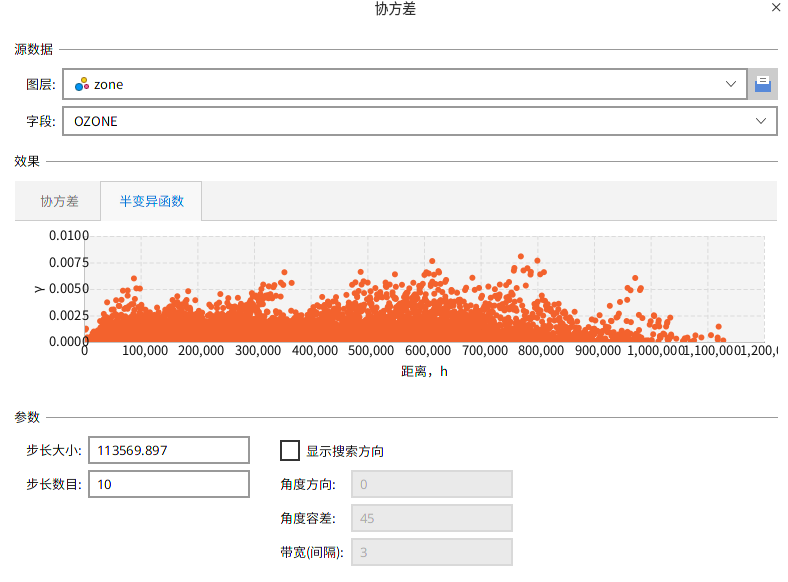
系统支持协方差函数分析，区域化随机变量之间的差异，可以用空间协方差来表示。协方差函数分析结果用云图显示，图形横轴表示两点之间的距离，纵轴表示两点之间的协方差值。

操作说明

1. 点击【地学统计】-【协方差分析】；

2. 在弹出的对话框中选择点简单要素类，设置分析的属性字段ozone；

3. 系统会自动计算分析结果。

• 【协方差】：表示任意两点间不同属性间的空间相关性程度，图形横轴表示两点之间的距离，纵轴表示两点之间的协方差值

• 【半变异函数】：表示任意两点间的空间相关性程度，图形横轴表示两点之间的距离，纵轴表示两点之间的变差函数值

通过半变异函数云图可看到随着距离逐渐拉大，任意两点间的空间相关性会变大，但距离达到一定程度后，任意两点间可能就不存在相关性。